17.02.2017

Το Excel είναι ένα υπολογιστικό φύλλο. Μπορεί να χρησιμοποιηθεί για τη δημιουργία ποικίλων αναφορών. Σε αυτό το πρόγραμμα, είναι πολύ βολικό να κάνετε διάφορους υπολογισμούς. Πολλοί δεν χρησιμοποιούν ούτε τις μισές δυνατότητες του Excel.

Ίσως χρειαστεί να βρείτε τη μέση τιμή των αριθμών στο σχολείο, καθώς και κατά τη διάρκεια της εργασίας. Με τον κλασικό τρόποΟ προσδιορισμός του αριθμητικού μέσου όρου χωρίς τη χρήση προγραμμάτων είναι να προσθέσετε όλους τους αριθμούς και στη συνέχεια το ποσό που προκύπτει πρέπει να διαιρεθεί με τον αριθμό των όρων. Εάν οι αριθμοί είναι αρκετά μεγάλοι ή εάν η λειτουργία πρέπει να εκτελεστεί πολλές φορές για λόγους αναφοράς, οι υπολογισμοί μπορεί να διαρκέσουν πολύ. Αυτό είναι μια παράλογη σπατάλη χρόνου και προσπάθειας, είναι πολύ καλύτερο να χρησιμοποιήσετε τις δυνατότητες του Excel.

Εύρεση του αριθμητικού μέσου όρου

Πολλά δεδομένα έχουν ήδη καταγραφεί αρχικά στο Excel, αλλά αν αυτό δεν συμβεί, είναι απαραίτητο να μεταφερθούν τα δεδομένα σε έναν πίνακα. Κάθε αριθμός για τον υπολογισμό πρέπει να βρίσκεται σε ξεχωριστό κελί.

Μέθοδος 1: Υπολογίστε τη μέση τιμή μέσω του "Οδηγού λειτουργιών"

Σε αυτή τη μέθοδο, πρέπει να γράψετε έναν τύπο για τον υπολογισμό του αριθμητικού μέσου όρου και να τον εφαρμόσετε στα καθορισμένα κελιά.

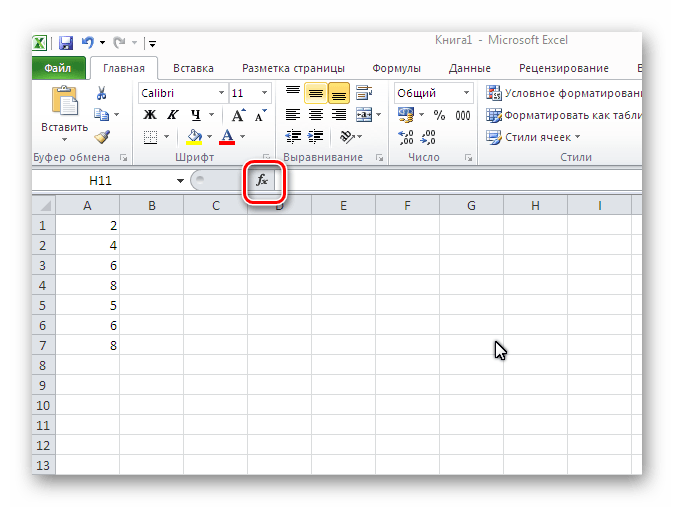
Το κύριο μειονέκτημα αυτής της μεθόδου είναι ότι πρέπει να εισάγετε μη αυτόματα κελιά για κάθε όρο. Υπό την παρουσία του ένας μεγάλος αριθμόςαριθμοί δεν είναι πολύ βολικό.

Μέθοδος 2: Αυτόματος υπολογισμός του αποτελέσματος σε επιλεγμένα κελιά

Σε αυτή τη μέθοδο, ο υπολογισμός του αριθμητικού μέσου όρου πραγματοποιείται με μερικά μόνο κλικ του ποντικιού. Πολύ βολικό για κάθε αριθμό αριθμών.

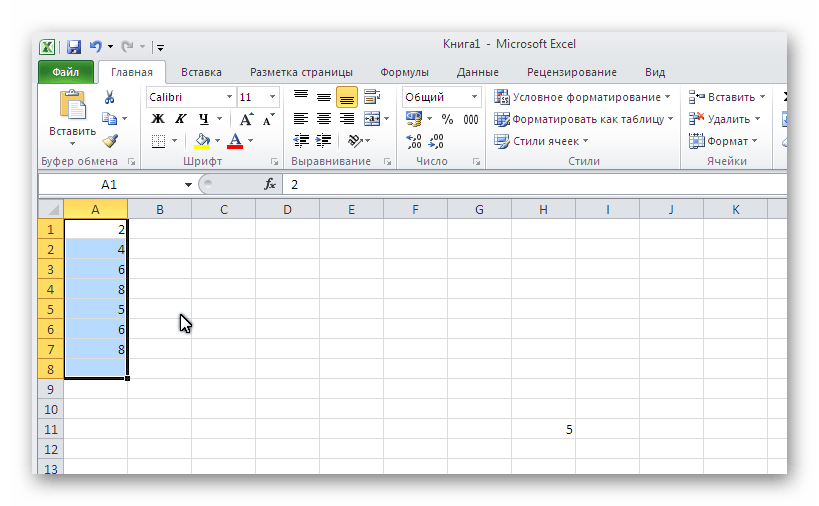
Το μειονέκτημα αυτής της μεθόδου είναι ο υπολογισμός της μέσης τιμής μόνο για αριθμούς που βρίσκονται κοντά. Εάν οι απαραίτητοι όροι είναι διάσπαρτοι, τότε δεν μπορούν να επιλεγούν για υπολογισμό. Δεν είναι καν δυνατή η επιλογή δύο στηλών, οπότε τα αποτελέσματα θα παρουσιάζονται ξεχωριστά για καθεμία από αυτές.

Μέθοδος 3: Χρησιμοποιώντας τη γραμμή τύπων

Ένας άλλος τρόπος για να μεταβείτε στο παράθυρο συνάρτησης:

Πλέον γρήγορο τρόπο, στο οποίο δεν χρειάζεται να κάνετε αναζήτηση για στοιχεία στο μενού για μεγάλο χρονικό διάστημα.

Μέθοδος 4: Χειροκίνητη καταχώριση

Δεν είναι απαραίτητο να χρησιμοποιήσετε τα εργαλεία στο μενού του Excel για τον υπολογισμό της μέσης τιμής, μπορείτε να γράψετε με μη αυτόματο τρόπο την απαραίτητη συνάρτηση.

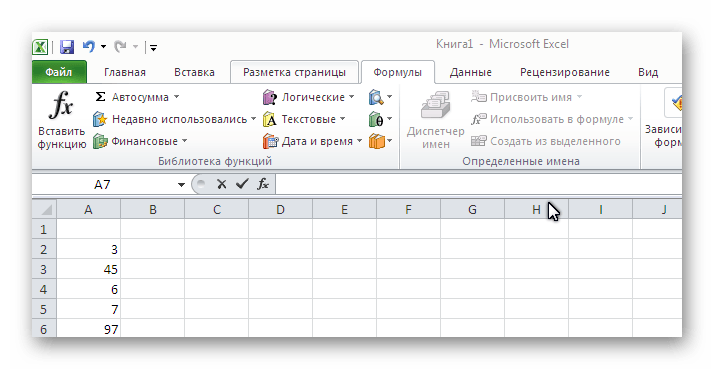
Γρήγορα και βολικό τρόπογια όσους προτιμούν να δημιουργούν τύπους με τα χέρια τους, αντί να αναζητούν έτοιμα προγράμματα στο μενού.

Χάρη σε αυτές τις δυνατότητες, είναι πολύ εύκολο να υπολογίσετε τη μέση τιμή οποιωνδήποτε αριθμών, ανεξάρτητα από τον αριθμό τους, ενώ μπορείτε επίσης να συντάξετε στατιστικά στοιχεία χωρίς να τα υπολογίσετε χειροκίνητα. Με τη βοήθεια των εργαλείων του προγράμματος Excel, οι οποιοιδήποτε υπολογισμοί γίνονται πολύ πιο εύκολοι από ό,τι στο μυαλό ή χρησιμοποιώντας μια αριθμομηχανή.

Για να βρείτε τη μέση τιμή στο Excel (είτε είναι αριθμητική, κείμενο, ποσοστό ή άλλη τιμή), υπάρχουν πολλές συναρτήσεις. Και καθένα από αυτά έχει τα δικά του χαρακτηριστικά και πλεονεκτήματα. Μετά από όλα, ορισμένες προϋποθέσεις μπορούν να τεθούν σε αυτήν την εργασία.

Για παράδειγμα, οι μέσες τιμές μιας σειράς αριθμών στο Excel υπολογίζονται χρησιμοποιώντας στατιστικές συναρτήσεις. Μπορείτε επίσης να εισαγάγετε χειροκίνητα τον δικό σας τύπο. Ας εξετάσουμε διάφορες επιλογές.

Πώς να βρείτε τον αριθμητικό μέσο όρο των αριθμών;

Για να βρείτε τον αριθμητικό μέσο όρο, προσθέτετε όλους τους αριθμούς του συνόλου και διαιρείτε το άθροισμα με τον αριθμό. Για παράδειγμα, οι βαθμοί ενός μαθητή στην επιστήμη των υπολογιστών: 3, 4, 3, 5, 5. Τι ισχύει για ένα τέταρτο: 4. Βρήκαμε τον αριθμητικό μέσο όρο χρησιμοποιώντας τον τύπο: \u003d (3 + 4 + 3 + 5 + 5) / 5.

Πώς να το κάνετε γρήγορα χρησιμοποιώντας τις συναρτήσεις του Excel; Πάρτε για παράδειγμα μια σειρά τυχαίων αριθμών σε μια συμβολοσειρά:

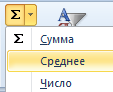
Ή: κάντε το κελί ενεργό και απλώς εισαγάγετε χειροκίνητα τον τύπο: =AVERAGE(A1:A8).

Τώρα ας δούμε τι άλλο μπορεί να κάνει η συνάρτηση AVERAGE.

Να βρείτε τον αριθμητικό μέσο όρο των δύο πρώτων και τριών τελευταίων αριθμών. Τύπος: =AVERAGE(A1:B1;F1:H1). Αποτέλεσμα:

Μέσος όρος κατά συνθήκη

Η προϋπόθεση για την εύρεση του αριθμητικού μέσου όρου μπορεί να είναι ένα αριθμητικό κριτήριο ή ένα κριτήριο κειμένου. Θα χρησιμοποιήσουμε τη συνάρτηση: =AVERAGEIF().

Να βρείτε τον αριθμητικό μέσο όρο αριθμών που είναι μεγαλύτεροι ή ίσοι του 10.

Συνάρτηση: =AVERAGEIF(A1:A8,">=10")

Το αποτέλεσμα της χρήσης της συνάρτησης AVERAGEIF στην συνθήκη ">=10":

Το τρίτο όρισμα - "Εύρος μέσου όρου" - παραλείπεται. Πρώτον, δεν απαιτείται. Δεύτερον, το εύρος που αναλύεται από το πρόγραμμα περιέχει ΜΟΝΟ αριθμητικές τιμές. Στα κελιά που καθορίζονται στο πρώτο όρισμα, η αναζήτηση θα εκτελεστεί σύμφωνα με τη συνθήκη που καθορίζεται στο δεύτερο όρισμα.

Προσοχή! Το κριτήριο αναζήτησης μπορεί να καθοριστεί σε ένα κελί. Και στον τύπο να γίνει αναφορά σε αυτό.

Ας βρούμε τη μέση τιμή των αριθμών με το κριτήριο του κειμένου. Για παράδειγμα, οι μέσες πωλήσεις του προϊόντος «πίνακες».

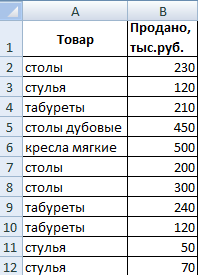
Η συνάρτηση θα μοιάζει με αυτό: =AVERAGEIF($A$2:$A$12;A7;$B$2:$B$12). Εύρος - μια στήλη με ονόματα προϊόντων. Το κριτήριο αναζήτησης είναι ένας σύνδεσμος προς ένα κελί με τη λέξη "πίνακες" (μπορείτε να εισαγάγετε τη λέξη "πίνακες" αντί του συνδέσμου A7). Εύρος μέσου όρου - αυτά τα κελιά από τα οποία θα ληφθούν δεδομένα για τον υπολογισμό της μέσης τιμής.

Ως αποτέλεσμα του υπολογισμού της συνάρτησης, λαμβάνουμε την ακόλουθη τιμή:

Προσοχή! Για ένα κριτήριο κειμένου (συνθήκη), πρέπει να καθοριστεί το μέσο εύρος τιμών.

Πώς να υπολογίσετε τη σταθμισμένη μέση τιμή στο Excel;

Πώς γνωρίζουμε τη σταθμισμένη μέση τιμή;

Τύπος: =SUMPRODUCT(C2:C12,B2:B12)/SUM(C2:C12).

Χρησιμοποιώντας τον τύπο SUMPRODUCT, ανακαλύπτουμε τα συνολικά έσοδα μετά την πώληση ολόκληρης της ποσότητας των αγαθών. Και η συνάρτηση SUM - συνοψίζει την ποσότητα των αγαθών. Διαιρώντας τα συνολικά έσοδα από την πώληση αγαθών με τον συνολικό αριθμό μονάδων αγαθών, βρήκαμε τη μέση σταθμισμένη τιμή. Αυτός ο δείκτης λαμβάνει υπόψη το «βάρος» κάθε τιμής. Το μερίδιό του στη συνολική μάζα των αξιών.

Τυπική απόκλιση: τύπος στο Excel

Διακρίνετε την τυπική απόκλιση για τον γενικό πληθυσμό και για το δείγμα. Στην πρώτη περίπτωση, αυτή είναι η ρίζα της γενικής διακύμανσης. Στη δεύτερη, από τη διακύμανση του δείγματος.

Για τον υπολογισμό αυτού του στατιστικού δείκτη, συντάσσεται ένας τύπος διασποράς. Η ρίζα λαμβάνεται από αυτό. Αλλά στο Excel υπάρχει μια έτοιμη συνάρτηση για την εύρεση της τυπικής απόκλισης.

Η τυπική απόκλιση συνδέεται με την κλίμακα των δεδομένων πηγής. Αυτό δεν αρκεί για μια εικονική αναπαράσταση της διακύμανσης του αναλυόμενου εύρους. Για να ληφθεί το σχετικό επίπεδο διασποράς στα δεδομένα, υπολογίζεται ο συντελεστής διακύμανσης:

τυπική απόκλιση / αριθμητικός μέσος όρος

Ο τύπος στο Excel μοιάζει με αυτό:

STDEV (εύρος τιμών) / AVERAGE (εύρος τιμών).

Ο συντελεστής διακύμανσης υπολογίζεται ως ποσοστό. Επομένως, ορίζουμε τη μορφή ποσοστού στο κελί.

Για επιτυχημένη λύσηΠρόβλημα 19 από το μέρος 3 πρέπει να γνωρίζετε μερικά Λειτουργίες Excel. Μία από αυτές τις λειτουργίες είναι ΜΕΣΗ ΤΙΜΗ. Ας το εξετάσουμε πιο αναλυτικά.

προέχωσας επιτρέπει να βρείτε τον αριθμητικό μέσο όρο των ορισμάτων. Η σύνταξη αυτής της συνάρτησης είναι:

AVERAGE (αριθμός 1, [αριθμός 2],…)

Μην ξεχνάτε ότι η εισαγωγή ενός τύπου σε ένα κελί ξεκινά με το σύμβολο "=".

Σε παρένθεση, μπορούμε να αναφέρουμε τους αριθμούς των οποίων τον μέσο όρο θέλουμε να βρούμε. Για παράδειγμα, αν γράψουμε σε ένα κελί =AVERAGE(1, 2, -7, 10, 7, 5, 9), τότε παίρνουμε 3,857142857. Αυτό είναι εύκολο να το ελέγξουμε - αν προσθέσουμε όλους τους αριθμούς σε αγκύλες (1 + 2 + (-7) + 10 + 7 + 5 + 9 = 27) και διαιρέσουμε με τον αριθμό τους (7), θα έχουμε 3,857142857142857.

Προσέξτε τους αριθμούς σε παρένθεση χωρίζονται με ερωτηματικό (; ). Έτσι, μπορούμε να καθορίσουμε έως και 255 αριθμούς.

Για παράδειγμα, χρησιμοποιώ το Microsort Excel 2010.

Επιπλέον, με τη βοήθεια Συναρτήσεις AVERAGEμπορούμε να βρούμε μέση τιμή μιας περιοχής κελιών. Ας υποθέσουμε ότι έχουμε αποθηκευμένους αριθμούς στην περιοχή A1:A7 και θέλουμε να βρούμε τον αριθμητικό μέσο όρο τους.

Ας βάλουμε στο κελί Β1 τον αριθμητικό μέσο όρο του εύρους A1:A7. Για να το κάνετε αυτό, τοποθετήστε τον κέρσορα στο κελί B1 και γράψτε =ΜΕΣΟΣ (A1:A7). Σε παρένθεση, υπέδειξα το εύρος των κελιών. Σημειώστε ότι ο οριοθέτης είναι ο χαρακτήρας άνω κάτω τελεία (: ). Θα ήταν ακόμα πιο εύκολο να γίνει - γράψτε στο κελί B1 =ΜΕΣΟΣ(και, στη συνέχεια, επιλέξτε το επιθυμητό εύρος με το ποντίκι.

Ως αποτέλεσμα, στο κελί B1 θα λάβουμε τον αριθμό 15.85714286 - αυτός είναι ο αριθμητικός μέσος όρος του εύρους A1:A7.

Ως προθέρμανση, προτείνω να βρούμε τη μέση τιμή των αριθμών από το 1 έως το 100 (1, 2, 3 κ.λπ. μέχρι το 100). Το πρώτο άτομο που θα απαντήσει σωστά στα σχόλια θα λάβει 50 ρούβλια στο τηλέφωνο Εργαζόμαστε.

Εντολή

Έστω ένα σύνολο τεσσάρων αριθμών. Πρέπει να βρεθεί μέση τιμή έννοιααυτό το σετ. Για να γίνει αυτό, βρίσκουμε πρώτα το άθροισμα όλων αυτών των αριθμών. Ας υποθέσουμε ότι αυτοί οι αριθμοί είναι 1, 3, 8, 7. Το άθροισμά τους είναι S = 1 + 3 + 8 + 7 = 19. Το σύνολο των αριθμών πρέπει να αποτελείται από αριθμούς του ίδιου πρόσημου, διαφορετικά η έννοια του υπολογισμού της μέσης τιμής είναι χαμένος.

Μέση τιμή έννοιασύνολο αριθμών ισούται με το άθροισμα των αριθμών S διαιρούμενο με τον αριθμό αυτών των αριθμών. Δηλαδή αποδεικνύεται ότι μέση τιμή έννοιαισούται με: 19/4 = 4,75.

Για να ορίσετε τον αριθμό μπορεί επίσης να βρεθεί όχι μόνο μέση τιμήαριθμητική, αλλά μέση τιμήγεωμετρικός. Ο γεωμετρικός μέσος όρος πολλών θετικών πραγματικών αριθμών είναι ένας αριθμός που μπορεί να αντικαταστήσει κάθε έναν από αυτούς τους αριθμούς, έτσι ώστε το γινόμενο τους να μην αλλάξει. Ο γεωμετρικός μέσος όρος G βρίσκεται με τον τύπο: η ρίζα του Νου βαθμού του γινομένου ενός συνόλου αριθμών, όπου N είναι ο αριθμός των αριθμών του συνόλου. Θεωρήστε το ίδιο σύνολο αριθμών: 1, 3, 8, 7. Βρείτε τους μέση τιμήγεωμετρικός. Για να γίνει αυτό, υπολογίζουμε το γινόμενο: 1 * 3 * 8 * 7 = 168. Τώρα από τον αριθμό 168 είναι απαραίτητο να εξαγάγετε τη ρίζα του 4ου βαθμού: G = (168) ^ 1/4 = 3,61. Με αυτόν τον τρόπο μέση τιμήτο γεωμετρικό σύνολο των αριθμών είναι 3,61.

Μέση τιμήο γεωμετρικός μέσος όρος χρησιμοποιείται γενικά λιγότερο συχνά από τον αριθμητικό μέσο όρο, αλλά μπορεί να είναι χρήσιμος κατά τον υπολογισμό του μέσου όρου των δεικτών που αλλάζουν με την πάροδο του χρόνου (μισθός ενός μεμονωμένου εργαζομένου, δυναμική ακαδημαϊκών επιδόσεων κ.λπ.).

Θα χρειαστείτε

• Μηχανική Αριθμομηχανή

Εντολή

Για να βρείτε το γεωμετρικό μέσο μιας σειράς αριθμών, πρέπει πρώτα να πολλαπλασιάσετε όλους αυτούς τους αριθμούς. Για παράδειγμα, σας δίνεται ένα σύνολο πέντε δεικτών: 12, 3, 6, 9 και 4. Ας πολλαπλασιάσουμε όλους αυτούς τους αριθμούς: 12x3x6x9x4=7776.

Τώρα, από τον αριθμό που προκύπτει, πρέπει να εξαγάγετε τη ρίζα του βαθμού ίση με τον αριθμό των στοιχείων της σειράς. Στην περίπτωσή μας, από τον αριθμό 7776, θα χρειαστεί να εξαγάγετε τη ρίζα πέμπτου βαθμού χρησιμοποιώντας μια αριθμομηχανή μηχανικής. Ο αριθμός που προκύπτει μετά από αυτή τη λειτουργία - σε αυτήν την περίπτωση ο αριθμός 6 - θα είναι ο γεωμετρικός μέσος όρος για την αρχική ομάδα αριθμών.

Εάν δεν διαθέτετε μηχανική αριθμομηχανή, μπορείτε να υπολογίσετε τον γεωμετρικό μέσο όρο μιας σειράς αριθμών χρησιμοποιώντας τη συνάρτηση CPGEOM στο Excel ή χρησιμοποιώντας μία από τις ηλεκτρονικές αριθμομηχανές που έχουν σχεδιαστεί ειδικά για τον υπολογισμό των μέσων γεωμετρικών τιμών.

Σημείωση

Εάν πρέπει να βρείτε τη γεωμετρική μέση τιμή για δύο μόνο αριθμούς, τότε δεν θα χρειαστείτε μηχανική αριθμομηχανή: μπορείτε να εξαγάγετε τη ρίζα δεύτερου βαθμού (τετραγωνική ρίζα) οποιουδήποτε αριθμού χρησιμοποιώντας την πιο κοινή αριθμομηχανή.

Χρήσιμες συμβουλές

Σε αντίθεση με τον αριθμητικό μέσο όρο, ο γεωμετρικός μέσος όρος δεν επηρεάζεται τόσο έντονα από μεγάλες αποκλίσεις και διακυμάνσεις μεταξύ των επιμέρους τιμών στο υπό μελέτη σύνολο δεικτών.

Πηγές:

• Ηλεκτρονική αριθμομηχανή που υπολογίζει τον γεωμετρικό μέσο όρο
• γεωμετρικός μέσος τύπος

Μέση τιμήΗ τιμή είναι ένα από τα χαρακτηριστικά ενός συνόλου αριθμών. Αντιπροσωπεύει έναν αριθμό που δεν μπορεί να είναι εκτός του εύρους που ορίζεται από τις μεγαλύτερες και τις μικρότερες τιμές σε αυτό το σύνολο αριθμών. Μέση τιμήαριθμητική τιμή - η πιο συχνά χρησιμοποιούμενη ποικιλία μέσων όρων.

Εντολή

Προσθέστε όλους τους αριθμούς του συνόλου και διαιρέστε τους με τον αριθμό των όρων για να πάρετε τον αριθμητικό μέσο όρο. Ανάλογα με τις συγκεκριμένες συνθήκες του υπολογισμού, μερικές φορές είναι ευκολότερο να διαιρέσουμε κάθε έναν από τους αριθμούς με τον αριθμό των τιμών στο σύνολο και να αθροίσουμε το αποτέλεσμα.

Χρησιμοποιήστε, για παράδειγμα, την αριθμομηχανή που περιλαμβάνεται στα Windows, εάν δεν μπορείτε να υπολογίσετε τον αριθμητικό μέσο όρο στο κεφάλι σας. Μπορείτε να το ανοίξετε χρησιμοποιώντας το παράθυρο διαλόγου εκκίνησης προγράμματος. Για να το κάνετε αυτό, πατήστε τα "πλήκτρα συντόμευσης" WIN + R ή κάντε κλικ στο κουμπί "Έναρξη" και επιλέξτε την εντολή "Εκτέλεση" από το κύριο μενού. Στη συνέχεια, πληκτρολογήστε calc στο πεδίο εισαγωγής και πατήστε Enter στο πληκτρολόγιο ή κάντε κλικ στο κουμπί OK. Το ίδιο μπορεί να γίνει μέσω του κύριου μενού - ανοίξτε το, μεταβείτε στην ενότητα "Όλα τα προγράμματα" και στην ενότητα "Τυπικό" και επιλέξτε τη γραμμή "Αριθμομηχανή".

Εισαγάγετε όλους τους αριθμούς του σετ διαδοχικά πατώντας το πλήκτρο Συν στο πληκτρολόγιο μετά από κάθε έναν από αυτούς (εκτός από τον τελευταίο) ή κάνοντας κλικ στο αντίστοιχο κουμπί στη διεπαφή της αριθμομηχανής. Μπορείτε επίσης να εισάγετε αριθμούς τόσο από το πληκτρολόγιο όσο και κάνοντας κλικ στα αντίστοιχα κουμπιά διεπαφής.

Πατήστε το πλήκτρο κάθετο ή κάντε κλικ σε αυτό το εικονίδιο στη διεπαφή της αριθμομηχανής αφού εισαγάγετε την τελευταία τιμή του συνόλου και εκτυπώστε τον αριθμό των αριθμών στη σειρά. Στη συνέχεια, πατήστε το σύμβολο ίσου και η αριθμομηχανή θα υπολογίσει και θα εμφανίσει τον αριθμητικό μέσο όρο.

Μπορείτε να χρησιμοποιήσετε έναν επεξεργαστή υπολογιστικών φύλλων για τον ίδιο σκοπό. Microsoft Excel. Σε αυτήν την περίπτωση, ξεκινήστε τον επεξεργαστή και εισαγάγετε όλες τις τιμές της ακολουθίας αριθμών σε γειτονικά κελιά. Εάν μετά την εισαγωγή κάθε αριθμού πατήσετε Enter ή το πλήκτρο κάτω ή δεξιό βέλος, ο ίδιος ο επεξεργαστής θα μετακινήσει την εστίαση εισόδου στο διπλανό κελί.

Επιλέξτε όλες τις εισαγόμενες τιμές και στην κάτω αριστερή γωνία του παραθύρου του επεξεργαστή (στη γραμμή κατάστασης) θα δείτε τον αριθμητικό μέσο όρο για τα επιλεγμένα κελιά.

Κάντε κλικ στο κελί δίπλα στον τελευταίο αριθμό που πληκτρολογήσατε, εάν δεν θέλετε να δείτε απλώς τον αριθμητικό μέσο όρο. Αναπτύξτε την αναπτυσσόμενη λίστα με την εικόνα του ελληνικού γράμματος σίγμα (Σ) στην ομάδα Επεξεργασία εντολών στην καρτέλα Αρχική σελίδα. Επιλέξτε τη γραμμή " Μέση τιμή” και ο επεξεργαστής θα εισαγάγει τον επιθυμητό τύπο για τον υπολογισμό του αριθμητικού μέσου όρου στο επιλεγμένο κελί. Πατήστε το πλήκτρο Enter και η τιμή θα υπολογιστεί.

Ο αριθμητικός μέσος όρος είναι ένα από τα μέτρα της κεντρικής τάσης, που χρησιμοποιείται ευρέως στα μαθηματικά και τους στατιστικούς υπολογισμούς. Η εύρεση του αριθμητικού μέσου όρου πολλών τιμών​​είναι πολύ απλή, αλλά κάθε εργασία έχει τις δικές της αποχρώσεις, τις οποίες είναι απλώς απαραίτητο να γνωρίζουμε για να εκτελέσουμε σωστούς υπολογισμούς.

Ποιος είναι ο αριθμητικός μέσος όρος

Ο αριθμητικός μέσος όρος καθορίζει τη μέση τιμή για ολόκληρο τον αρχικό πίνακα αριθμών. Με άλλα λόγια, από ένα συγκεκριμένο σύνολο αριθμών, επιλέγεται μια τιμή κοινή για όλα τα στοιχεία, η μαθηματική σύγκριση της οποίας με όλα τα στοιχεία είναι περίπου ίση. Ο αριθμητικός μέσος όρος χρησιμοποιείται κυρίως για την προετοιμασία οικονομικών και στατιστικών αναφορών ή για τον υπολογισμό των ποσοτικών αποτελεσμάτων τέτοιων πειραμάτων.

Πώς να βρείτε τον αριθμητικό μέσο όρο

Η αναζήτηση για τον αριθμητικό μέσο όρο για έναν πίνακα αριθμών θα πρέπει να ξεκινήσει με τον προσδιορισμό του αλγεβρικού αθροίσματος αυτών των τιμών. Για παράδειγμα, εάν ο πίνακας περιέχει τους αριθμούς 23, 43, 10, 74 και 34, τότε το αλγεβρικό άθροισμά τους θα είναι 184. Κατά τη γραφή, ο αριθμητικός μέσος όρος συμβολίζεται με το γράμμα μ (mu) ή x (x με ράβδο) . Στη συνέχεια, το αλγεβρικό άθροισμα πρέπει να διαιρεθεί με τον αριθμό των αριθμών του πίνακα. Σε αυτό το παράδειγμα, υπήρχαν πέντε αριθμοί, οπότε ο αριθμητικός μέσος όρος θα είναι 184/5 και θα είναι 36,8.

Χαρακτηριστικά της εργασίας με αρνητικούς αριθμούς

Εάν υπάρχουν αρνητικοί αριθμοί στον πίνακα, τότε ο αριθμητικός μέσος όρος βρίσκεται χρησιμοποιώντας έναν παρόμοιο αλγόριθμο. Υπάρχει διαφορά μόνο κατά τον υπολογισμό στο περιβάλλον προγραμματισμού ή εάν υπάρχουν πρόσθετες συνθήκες στην εργασία. Σε αυτές τις περιπτώσεις, η εύρεση του αριθμητικού μέσου όρου αριθμών με διαφορετικά πρόσημα καταλήγει σε τρία βήματα:

1. Εύρεση του κοινού αριθμητικού μέσου όρου με την τυπική μέθοδο.
2. Εύρεση του αριθμητικού μέσου όρου των αρνητικών αριθμών.
3. Υπολογισμός του αριθμητικού μέσου όρου των θετικών αριθμών.

Οι απαντήσεις καθεμιάς από τις ενέργειες γράφονται χωρισμένες με κόμμα.

Φυσικά και δεκαδικά κλάσματα

Εάν ο πίνακας αριθμών παριστάνεται με δεκαδικά κλάσματα, η λύση εμφανίζεται σύμφωνα με τη μέθοδο υπολογισμού του αριθμητικού μέσου όρου των ακεραίων, αλλά το αποτέλεσμα μειώνεται σύμφωνα με τις απαιτήσεις του προβλήματος για την ακρίβεια της απάντησης.

Όταν εργάζεστε με φυσικά κλάσματα, θα πρέπει να μειωθούν σε έναν κοινό παρονομαστή, ο οποίος πολλαπλασιάζεται με τον αριθμό των αριθμών του πίνακα. Ο αριθμητής της απάντησης θα είναι το άθροισμα των δεδομένων αριθμητών των αρχικών κλασματικών στοιχείων.

Ο γεωμετρικός μέσος όρος των αριθμών εξαρτάται όχι μόνο από την απόλυτη τιμή των ίδιων των αριθμών, αλλά και από τον αριθμό τους. Μην μπερδεύετε τον γεωμετρικό μέσο και τον αριθμητικό μέσο όρο των αριθμών, καθώς βρίσκονται με διαφορετικές μεθόδους. Ο γεωμετρικός μέσος όρος είναι πάντα μικρότερος ή ίσος με τον αριθμητικό μέσο όρο.

Για να βρείτε τον γεωμετρικό μέσο όρο περισσότερων από δύο αριθμών, χρησιμοποιήστε επίσης τον βασικό κανόνα. Για να το κάνετε αυτό, βρείτε το γινόμενο όλων των αριθμών για τους οποίους θέλετε να βρείτε τη γεωμετρική μέση τιμή. Από το προϊόν που προκύπτει, εξάγετε τη ρίζα του βαθμού ίση με τον αριθμό των αριθμών. Για παράδειγμα, για να βρείτε το γεωμετρικό μέσο των αριθμών 2, 4 και 64, βρείτε το γινόμενο τους. 2•4•64=512. Εφόσον πρέπει να βρείτε το αποτέλεσμα του γεωμετρικού μέσου όρου τριών αριθμών, εξάγετε τη ρίζα του τρίτου βαθμού από το γινόμενο. Είναι δύσκολο να το κάνετε αυτό προφορικά, γι' αυτό χρησιμοποιήστε μια αριθμομηχανή μηχανικής. Για να γίνει αυτό, έχει ένα κουμπί "x ^ y". Καλέστε τον αριθμό 512, πατήστε το κουμπί "x^y", μετά πληκτρολογήστε τον αριθμό 3 και πατήστε το κουμπί "1/x", για να βρείτε την τιμή 1/3, πατήστε το κουμπί "=". Παίρνουμε το αποτέλεσμα της αύξησης του 512 στη δύναμη του 1/3, που αντιστοιχεί στη ρίζα του τρίτου βαθμού. Λάβετε 512^1/3=8. Αυτός είναι ο γεωμετρικός μέσος όρος των αριθμών 2.4 και 64.

Χρησιμοποιώντας μια αριθμομηχανή μηχανικής, μπορείτε να βρείτε το γεωμετρικό μέσο με άλλο τρόπο. Βρείτε το κουμπί καταγραφής στο πληκτρολόγιό σας. Μετά από αυτό, πάρτε τον λογάριθμο για κάθε έναν από τους αριθμούς, βρείτε το άθροισμά τους και διαιρέστε το με τον αριθμό των αριθμών. Από τον αριθμό που προκύπτει, πάρτε τον αντιλογάριθμο. Αυτός θα είναι ο γεωμετρικός μέσος όρος των αριθμών. Για παράδειγμα, για να βρείτε το γεωμετρικό μέσο των ίδιων αριθμών 2, 4 και 64, κάντε ένα σύνολο πράξεων στην αριθμομηχανή. Πληκτρολογήστε τον αριθμό 2, μετά πατήστε το κουμπί καταγραφής, πατήστε το κουμπί "+", πληκτρολογήστε τον αριθμό 4 και πατήστε ξανά log και "+", πληκτρολογήστε 64, πατήστε log και "=". Το αποτέλεσμα θα είναι ένας αριθμός ίσος με το άθροισμα των δεκαδικών λογαρίθμων των αριθμών 2, 4 και 64. Διαιρέστε τον αριθμό που προκύπτει με το 3, αφού αυτός είναι ο αριθμός των αριθμών με τους οποίους αναζητείται ο γεωμετρικός μέσος όρος. Από το αποτέλεσμα, πάρτε τον αντιλογάριθμο εναλλάσσοντας το κλειδί εγγραφής και χρησιμοποιήστε το ίδιο κλειδί καταγραφής. Το αποτέλεσμα είναι ο αριθμός 8, αυτός είναι ο επιθυμητός γεωμετρικός μέσος όρος.

Σημείωση

Ο μέσος όρος δεν μπορεί να είναι μεγαλύτερος από τον μεγαλύτερο αριθμό στο σύνολο και μικρότερος από τον μικρότερο.

Χρήσιμες συμβουλές

Στη μαθηματική στατιστική, η μέση τιμή μιας ποσότητας ονομάζεται μαθηματική προσδοκία.

Πηγές:

• πώς να υπολογίσετε τον μέσο όρο
• Βρείτε τον αριθμητικό μέσο όρο όλων των ακεραίων από το 1 έως το 1000
• Εύρεση του γεωμετρικού μέσου όρου

Στις περισσότερες περιπτώσεις, τα δεδομένα συγκεντρώνονται γύρω από κάποιο κεντρικό σημείο. Έτσι, για να περιγράψουμε οποιοδήποτε σύνολο δεδομένων, αρκεί να υποδείξουμε τη μέση τιμή. Εξετάστε διαδοχικά τρία αριθμητικά χαρακτηριστικά που χρησιμοποιούνται για την εκτίμηση της μέσης τιμής της κατανομής: αριθμητικός μέσος όρος, διάμεσος και τρόπος λειτουργίας.

Μέση τιμή

Ο αριθμητικός μέσος όρος (συχνά αναφέρεται απλώς ως μέσος όρος) είναι η πιο κοινή εκτίμηση του μέσου όρου μιας κατανομής. Είναι το αποτέλεσμα της διαίρεσης του αθροίσματος όλων των παρατηρούμενων αριθμητικών τιμών με τον αριθμό τους. Για ένα δείγμα αριθμών Χ 1, Χ 2, ..., Χn, ο μέσος όρος του δείγματος (σημειώνεται με το σύμβολο ) ισοδυναμεί \u003d (X 1 + X 2 + ... + Xn) / n, ή

πού είναι ο μέσος όρος του δείγματος, n- το μέγεθος του δείγματος, ΧΕγώ – i-ο στοιχείοδείγματα.

Λήψη σημείωσης σε ή μορφή, παραδείγματα σε μορφή

Εξετάστε το ενδεχόμενο να υπολογίσετε τον αριθμητικό μέσο όρο των πενταετών μέσων ετήσιων αποδόσεων 15 αμοιβαίων κεφαλαίων πολύ υψηλού κινδύνου (Εικόνα 1).

Ρύζι. 1. Μέση ετήσια απόδοση 15 αμοιβαίων κεφαλαίων πολύ υψηλού κινδύνου

Ο μέσος όρος του δείγματος υπολογίζεται ως εξής:

Αυτή είναι μια καλή απόδοση, ειδικά σε σύγκριση με την απόδοση 3-4% που έλαβαν οι καταθέτες τραπεζών ή πιστωτικών ενώσεων την ίδια χρονική περίοδο. Εάν ταξινομήσετε τις τιμές απόδοσης, είναι εύκολο να δείτε ότι οκτώ αμοιβαία κεφάλαια έχουν απόδοση πάνω από το μέσο όρο και επτά - κάτω από το μέσο όρο. Ο αριθμητικός μέσος όρος λειτουργεί ως σημείο ισορροπίας, έτσι ώστε τα κεφάλαια χαμηλού εισοδήματος να εξισορροπούν τα κεφάλαια υψηλού εισοδήματος. Όλα τα στοιχεία του δείγματος εμπλέκονται στον υπολογισμό του μέσου όρου. Κανένας από τους άλλους εκτιμητές του μέσου όρου κατανομής δεν έχει αυτήν την ιδιότητα.

Πότε να υπολογίσετε τον αριθμητικό μέσο όρο.Δεδομένου ότι ο αριθμητικός μέσος όρος εξαρτάται από όλα τα στοιχεία του δείγματος, η παρουσία ακραίων τιμών επηρεάζει σημαντικά το αποτέλεσμα. Σε τέτοιες περιπτώσεις, ο αριθμητικός μέσος όρος μπορεί να παραμορφώσει την έννοια των αριθμητικών δεδομένων. Επομένως, κατά την περιγραφή ενός συνόλου δεδομένων που περιέχει ακραίες τιμές, είναι απαραίτητο να υποδεικνύεται η διάμεσος ή ο αριθμητικός μέσος όρος και η διάμεσος. Για παράδειγμα, εάν η απόδοση του αμοιβαίου κεφαλαίου της Αναδυόμενης Ανάπτυξης της RS αφαιρεθεί από το δείγμα, ο μέσος όρος του δείγματος της απόδοσης των 14 κεφαλαίων μειώνεται σχεδόν κατά 1% σε 5,19%.

Διάμεσος

Η διάμεσος είναι η μεσαία τιμή ενός διατεταγμένου πίνακα αριθμών. Εάν ο πίνακας δεν περιέχει επαναλαμβανόμενους αριθμούς, τότε τα μισά στοιχεία του θα είναι μικρότερα και μισά περισσότερα από τη διάμεσο. Εάν το δείγμα περιέχει ακραίες τιμές, είναι προτιμότερο να χρησιμοποιηθεί η διάμεσος παρά ο αριθμητικός μέσος όρος για την εκτίμηση του μέσου όρου. Για να υπολογιστεί η διάμεσος ενός δείγματος, πρέπει πρώτα να ταξινομηθεί.

Αυτή η φόρμουλα είναι διφορούμενη. Το αποτέλεσμά του εξαρτάται από το αν ο αριθμός είναι άρτιος ή μονός. n:

• Εάν το δείγμα περιέχει μονό αριθμό στοιχείων, η διάμεσος είναι (n+1)/2-ο στοιχείο.
• Εάν το δείγμα περιέχει ζυγό αριθμό στοιχείων, η διάμεσος βρίσκεται μεταξύ των δύο μεσαίων στοιχείων του δείγματος και είναι ίση με τον αριθμητικό μέσο όρο που υπολογίζεται σε αυτά τα δύο στοιχεία.

Για να υπολογίσουμε τη διάμεση τιμή για ένα δείγμα 15 αμοιβαίων κεφαλαίων πολύ υψηλού κινδύνου, πρέπει πρώτα να ταξινομήσουμε τα πρωτογενή δεδομένα (Εικόνα 2). Τότε η διάμεσος θα είναι απέναντι από τον αριθμό του μεσαίου στοιχείου του δείγματος. στο παράδειγμά μας με αριθμό 8. Το Excel έχει μια ειδική συνάρτηση =MEDIAN() που λειτουργεί και με μη ταξινομημένους πίνακες.

Ρύζι. 2. Διάμεσος 15 ταμεία

Έτσι, η διάμεσος είναι 6,5. Αυτό σημαίνει ότι τα μισά από τα κεφάλαια πολύ υψηλού κινδύνου δεν ξεπερνούν τα 6,5, ενώ τα άλλα μισά το κάνουν. Σημειώστε ότι η διάμεσος του 6,5 είναι ελαφρώς μεγαλύτερη από τη διάμεσο του 6,08.

Εάν αφαιρέσουμε την κερδοφορία του RS Emerging Growth fund από το δείγμα, τότε η διάμεσος των υπόλοιπων 14 αμοιβαίων κεφαλαίων θα μειωθεί στο 6,2%, δηλαδή όχι τόσο σημαντικά όσο ο αριθμητικός μέσος όρος (Εικ. 3).

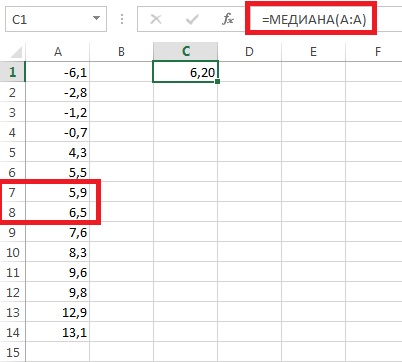
Ρύζι. 3. Διάμεσος 14 ταμεία

Μόδα

Ο όρος εισήχθη για πρώτη φορά από τον Pearson το 1894. Η μόδα είναι ο αριθμός που εμφανίζεται πιο συχνά στο δείγμα (το πιο μοδάτο). Η μόδα περιγράφει καλά, για παράδειγμα, την τυπική αντίδραση των οδηγών σε ένα σήμα κυκλοφορίας για διακοπή της κυκλοφορίας. Ένα κλασικό παράδειγμα χρήσης της μόδας είναι η επιλογή του μεγέθους της παραγόμενης παρτίδας παπουτσιών ή του χρώματος της ταπετσαρίας. Εάν μια διανομή έχει πολλαπλούς τρόπους λειτουργίας, τότε λέγεται ότι είναι πολυτροπική ή πολυτροπική (έχει δύο ή περισσότερες "κορυφές"). Η πολυτροπικότητα της διανομής δίνει σημαντικές πληροφορίεςσχετικά με τη φύση της υπό μελέτη μεταβλητής. Για παράδειγμα, σε κοινωνιολογικές έρευνες, εάν μια μεταβλητή αντιπροσωπεύει μια προτίμηση ή στάση απέναντι σε κάτι, τότε η πολυτροπικότητα θα μπορούσε να σημαίνει ότι υπάρχουν πολλές σαφώς διαφορετικές απόψεις. Η πολυτροπικότητα είναι επίσης ένας δείκτης ότι το δείγμα δεν είναι ομοιογενές και ότι οι παρατηρήσεις μπορεί να δημιουργηθούν από δύο ή περισσότερες «επικαλυπτόμενες» κατανομές. Σε αντίθεση με τον αριθμητικό μέσο όρο, οι ακραίες τιμές δεν επηρεάζουν τη λειτουργία. Για τυχαίες μεταβλητές που κατανέμονται συνεχώς, όπως οι μέσες ετήσιες αποδόσεις των αμοιβαίων κεφαλαίων, η λειτουργία μερικές φορές δεν υπάρχει καθόλου (ή δεν έχει νόημα). Δεδομένου ότι αυτοί οι δείκτες μπορούν να λάβουν μια ποικιλία τιμών, οι επαναλαμβανόμενες τιμές είναι εξαιρετικά σπάνιες.

τεταρτημόρια

Τα τεταρτημόρια είναι μέτρα που χρησιμοποιούνται πιο συχνά για την αξιολόγηση της κατανομής των δεδομένων κατά την περιγραφή των ιδιοτήτων μεγάλων αριθμητικών δειγμάτων. Ενώ η διάμεσος χωρίζει τον ταξινομημένο πίνακα στο μισό (50% των στοιχείων του πίνακα είναι λιγότερα από το διάμεσο και το 50% είναι μεγαλύτερα), τα τεταρτημόρια διαχωρίζουν το ταξινομημένο σύνολο δεδομένων σε τέσσερα μέρη. Οι τιμές Q 1 , διάμεσος και Q 3 είναι το 25ο, 50ο και 75ο εκατοστημόριο, αντίστοιχα. Το πρώτο τεταρτημόριο Q 1 είναι ένας αριθμός που χωρίζει το δείγμα σε δύο μέρη: το 25% των στοιχείων είναι μικρότερα από και το 75% είναι περισσότερα από το πρώτο τεταρτημόριο.

Το τρίτο τεταρτημόριο Q 3 είναι ένας αριθμός που χωρίζει επίσης το δείγμα σε δύο μέρη: το 75% των στοιχείων είναι μικρότερα από και το 25% είναι περισσότερα από το τρίτο τεταρτημόριο.

Για τον υπολογισμό τεταρτημορίων σε εκδόσεις του Excel πριν από το 2007, χρησιμοποιήθηκε η συνάρτηση =QUARTILE (πίνακας, τμήμα). Ξεκινώντας με το Excel 2010, ισχύουν δύο λειτουργίες:

• =QUARTILE.ON (πίνακας, τμήμα)
• =QUARTILE.EXC(πίνακας, μέρος)

Αυτές οι δύο συναρτήσεις δίνουν ελαφρώς διαφορετικές τιμές (Εικόνα 4). Για παράδειγμα, κατά τον υπολογισμό των τεταρτημορίων ενός δείγματος που περιέχει δεδομένα για τη μέση ετήσια απόδοση 15 αμοιβαίων κεφαλαίων πολύ υψηλού κινδύνου, Q 1 = 1,8 ή -0,7 για QUARTILE.INC και QUARTILE.EXC, αντίστοιχα. Παρεμπιπτόντως, η συνάρτηση QUARTILE που χρησιμοποιήθηκε νωρίτερα αντιστοιχεί στη σύγχρονη συνάρτηση QUARTILE.ON. Για να υπολογίσετε τεταρτημόρια στο Excel χρησιμοποιώντας τους παραπάνω τύπους, ο πίνακας δεδομένων μπορεί να παραμείνει χωρίς σειρά.

Ρύζι. 4. Υπολογίστε τεταρτημόρια στο Excel

Να τονίσουμε ξανά. Το Excel μπορεί να υπολογίσει τεταρτημόρια για μονομεταβλητή διακριτές σειρές, που περιέχει τις τιμές μιας τυχαίας μεταβλητής. Ο υπολογισμός των τεταρτημορίων για μια κατανομή με βάση τη συχνότητα δίνεται στην παρακάτω ενότητα.

γεωμετρικό μέσο

Σε αντίθεση με τον αριθμητικό μέσο όρο, ο γεωμετρικός μέσος όρος μετρά πόσο έχει αλλάξει μια μεταβλητή με την πάροδο του χρόνου. Το γεωμετρικό μέσο είναι η ρίζα nου βαθμού από το προϊόν nτιμές (στο Excel, χρησιμοποιείται η συνάρτηση = CUGEOM):

σολ= (X 1 * X 2 * ... * X n) 1/n

Μια παρόμοια παράμετρος - ο γεωμετρικός μέσος όρος του ρυθμού απόδοσης - καθορίζεται από τον τύπο:

G \u003d [(1 + R 1) * (1 + R 2) * ... * (1 + R n)] 1 / n - 1,

όπου R i- ποσοστό απόδοσης Εγώ-η χρονική περίοδος.

Για παράδειγμα, ας υποθέσουμε ότι η αρχική επένδυση είναι 100.000 $. Μέχρι το τέλος του πρώτου έτους, πέφτει στα 50.000 $ και μέχρι το τέλος του δεύτερου έτους, επανέρχεται στα αρχικά 100.000 $. Το ποσοστό απόδοσης αυτής της επένδυσης σε διάστημα δύο περίοδος έτους είναι ίση με 0, αφού το αρχικό και το τελικό ποσό των κεφαλαίων είναι ίσα μεταξύ τους. Ωστόσο, ο αριθμητικός μέσος όρος των ετήσιων ποσοστών απόδοσης είναι = (-0,5 + 1) / 2 = 0,25 ή 25%, δεδομένου ότι το ποσοστό απόδοσης το πρώτο έτος R 1 = (50.000 - 100.000) / 100.000 = -0,5 , και στο δεύτερο R 2 = (100.000 - 50.000) / 50.000 = 1. Ταυτόχρονα, ο γεωμετρικός μέσος όρος του ποσοστού απόδοσης για δύο χρόνια είναι: G = [(1–0,5) * (1 + 1 )] 1 /2 – 1 = ½ – 1 = 1 – 1 = 0. Έτσι, ο γεωμετρικός μέσος όρος αντικατοπτρίζει με μεγαλύτερη ακρίβεια τη μεταβολή (ακριβέστερα, την απουσία αλλαγής) στον όγκο των επενδύσεων κατά τη διετία από τον αριθμητικό μέσο όρο.

Ενδιαφέροντα γεγονότα.Πρώτον, ο γεωμετρικός μέσος όρος θα είναι πάντα μικρότερος από τον αριθμητικό μέσο όρο των ίδιων αριθμών. Εκτός από την περίπτωση που όλοι οι αριθμοί που λαμβάνονται είναι ίσοι μεταξύ τους. Δεύτερον, έχοντας εξετάσει τις ιδιότητες ενός ορθογωνίου τριγώνου, μπορεί κανείς να καταλάβει γιατί ο μέσος όρος ονομάζεται γεωμετρικός. Το ύψος ενός ορθογώνιου τριγώνου, χαμηλωμένο στην υποτείνουσα, είναι η μέση αναλογία μεταξύ των προεξοχών των ποδιών στην υποτείνουσα, και κάθε σκέλος είναι η μέση αναλογία μεταξύ της υποτείνουσας και της προβολής της στην υποτείνουσα (Εικ. 5). Αυτό δίνει έναν γεωμετρικό τρόπο κατασκευής του γεωμετρικού μέσου όρου δύο (μήκη) τμημάτων: πρέπει να χτίσετε έναν κύκλο στο άθροισμα αυτών των δύο τμημάτων ως διάμετρο και, στη συνέχεια, το ύψος, που θα αποκατασταθεί από το σημείο της σύνδεσής τους στη διασταύρωση με το κύκλος, θα δώσει την απαιτούμενη τιμή:

Ρύζι. 5. Η γεωμετρική φύση του γεωμετρικού μέσου (σχήμα από τη Wikipedia)

Η δεύτερη σημαντική ιδιότητα των αριθμητικών δεδομένων είναι το δικό τους παραλλαγήχαρακτηρίζοντας το βαθμό διασποράς των δεδομένων. Δύο διαφορετικά δείγματα μπορεί να διαφέρουν τόσο σε μέσες τιμές όσο και σε παραλλαγές. Ωστόσο, όπως φαίνεται στο σχ. 6 και 7, δύο δείγματα μπορεί να έχουν την ίδια παραλλαγή αλλά διαφορετικά μέσα ή τον ίδιο μέσο όρο και εντελώς διαφορετική παραλλαγή. Τα δεδομένα που αντιστοιχούν στο πολύγωνο Β στο Σχ. 7 αλλάζουν πολύ λιγότερο από τα δεδομένα από τα οποία κατασκευάστηκε το πολύγωνο Α.

Ρύζι. 6. Δύο συμμετρικές κατανομές σε σχήμα καμπάνας με το ίδιο spread και διαφορετικές μέσες τιμές

Ρύζι. 7. Δύο συμμετρικές κατανομές σε σχήμα καμπάνας με τις ίδιες μέσες τιμές και διαφορετική διασπορά

Υπάρχουν πέντε εκτιμήσεις της διακύμανσης των δεδομένων:

• σπιθαμή,
• διατεταρτημοριακό εύρος,
• διασπορά,
• τυπική απόκλιση,
• ο συντελεστής διακύμανσης.

πεδίο εφαρμογής

Το εύρος είναι η διαφορά μεταξύ του μεγαλύτερου και του μικρότερου στοιχείου του δείγματος:

Σύρετε = XMax-XΕλάχ

Το εύρος ενός δείγματος που περιέχει τις μέσες ετήσιες αποδόσεις 15 αμοιβαίων κεφαλαίων πολύ υψηλού κινδύνου μπορεί να υπολογιστεί χρησιμοποιώντας έναν ταξινομημένο πίνακα (βλ. Εικόνα 4): εύρος = 18,5 - (-6,1) = 24,6. Αυτό σημαίνει ότι η διαφορά μεταξύ της υψηλότερης και της χαμηλότερης μέσης ετήσιας απόδοσης για αμοιβαία κεφάλαια πολύ υψηλού κινδύνου είναι 24,6%.

Το εύρος μετρά τη συνολική εξάπλωση των δεδομένων. Αν και το εύρος του δείγματος είναι μια πολύ απλή εκτίμηση της συνολικής εξάπλωσης των δεδομένων, η αδυναμία του είναι ότι δεν λαμβάνει υπόψη ακριβώς τον τρόπο κατανομής των δεδομένων μεταξύ του ελάχιστου και του μέγιστου στοιχείου. Αυτό το αποτέλεσμα φαίνεται καλά στο Σχ. 8 που απεικονίζει δείγματα που έχουν το ίδιο εύρος. Η κλίμακα Β δείχνει ότι εάν το δείγμα περιέχει τουλάχιστον μία ακραία τιμή, το εύρος του δείγματος είναι μια πολύ ανακριβής εκτίμηση της διασποράς των δεδομένων.

Ρύζι. 8. Σύγκριση τριών δειγμάτων με το ίδιο εύρος. το τρίγωνο συμβολίζει την υποστήριξη της ισορροπίας και η θέση του αντιστοιχεί στη μέση τιμή του δείγματος

Διατεταρτημοριακό εύρος

Το διατεταρτημόριο ή το μέσο εύρος είναι η διαφορά μεταξύ του τρίτου και του πρώτου τεταρτημορίου του δείγματος:

Εύρος διατεταρτημορίου \u003d Q 3 - Q 1

Αυτή η τιμή καθιστά δυνατό να εκτιμηθεί η εξάπλωση του 50% των στοιχείων και να μην ληφθεί υπόψη η επίδραση των ακραίων στοιχείων. Το διατεταρτημόριο για ένα δείγμα που περιέχει δεδομένα για τις μέσες ετήσιες αποδόσεις 15 αμοιβαίων κεφαλαίων πολύ υψηλού κινδύνου μπορεί να υπολογιστεί χρησιμοποιώντας τα δεδομένα στο Σχήμα. 4 (για παράδειγμα, για τη συνάρτηση QUARTILE.EXC): Εύρος διατεταρτημορίου = 9,8 - (-0,7) = 10,5. Το διάστημα μεταξύ 9,8 και -0,7 αναφέρεται συχνά ως μεσαίο μισό.

Πρέπει να σημειωθεί ότι οι τιμές Q 1 και Q 3, και ως εκ τούτου το διατεταρτημόριο, δεν εξαρτώνται από την παρουσία ακραίων τιμών, καθώς ο υπολογισμός τους δεν λαμβάνει υπόψη καμία τιμή μικρότερη από Q 1 ή μεγαλύτερη από Q 3 . Τα συνολικά ποσοτικά χαρακτηριστικά, όπως η διάμεσος, το πρώτο και το τρίτο τεταρτημόριο και το διατεταρτημόριο, τα οποία δεν επηρεάζονται από ακραίες τιμές, ονομάζονται ισχυροί δείκτες.

Ενώ το εύρος και το διατεταρτημόριο εύρος παρέχουν μια εκτίμηση της συνολικής και της μέσης διασποράς του δείγματος, αντίστοιχα, καμία από αυτές τις εκτιμήσεις δεν λαμβάνει υπόψη ακριβώς τον τρόπο με τον οποίο κατανέμονται τα δεδομένα. Διακύμανση και τυπική απόκλισηαπαλλαγμένο από αυτό το μειονέκτημα. Αυτοί οι δείκτες σάς επιτρέπουν να αξιολογήσετε τον βαθμό διακύμανσης των δεδομένων γύρω από τον μέσο όρο. Διακύμανση δείγματοςείναι μια προσέγγιση του αριθμητικού μέσου όρου που υπολογίζεται από τις τετραγωνικές διαφορές μεταξύ κάθε στοιχείου δείγματος και του μέσου όρου του δείγματος. Για ένα δείγμα X 1 , X 2 , ... X n η διακύμανση του δείγματος (που συμβολίζεται με το σύμβολο S 2 δίνεται με τον ακόλουθο τύπο:

Γενικά, η διακύμανση του δείγματος είναι το άθροισμα των τετραγωνικών διαφορών μεταξύ των στοιχείων του δείγματος και του μέσου όρου του δείγματος, διαιρούμενο με μια τιμή ίση με το μέγεθος του δείγματος μείον ένα:

όπου - αριθμητικός μέσος όρος, n- το μέγεθος του δείγματος, X i - Εγώ-ο δείγμα στοιχείου Χ. Στο Excel πριν από την έκδοση 2007, η συνάρτηση =VAR() χρησιμοποιήθηκε για τον υπολογισμό της διακύμανσης του δείγματος, από την έκδοση 2010, χρησιμοποιείται η συνάρτηση =VAR.V().

Η πιο πρακτική και ευρέως αποδεκτή εκτίμηση της διασποράς δεδομένων είναι τυπική απόκλιση. Αυτός ο δείκτης συμβολίζεται με το σύμβολο S και ισούται με την τετραγωνική ρίζα της διακύμανσης του δείγματος:

Στο Excel πριν από την έκδοση 2007, η συνάρτηση =STDEV() χρησιμοποιήθηκε για τον υπολογισμό της τυπικής απόκλισης, από την έκδοση 2010 χρησιμοποιείται η συνάρτηση =STDEV.V(). Για τον υπολογισμό αυτών των συναρτήσεων, ο πίνακας δεδομένων μπορεί να είναι μη ταξινομημένος.

Ούτε η διακύμανση του δείγματος ούτε η τυπική απόκλιση του δείγματος μπορεί να είναι αρνητικές. Η μόνη περίπτωση στην οποία οι δείκτες S 2 και S μπορούν να είναι μηδενικοί είναι εάν όλα τα στοιχεία του δείγματος είναι ίσα. Σε αυτή την εντελώς απίθανη περίπτωση, το εύρος και το εύρος του διατεταρτημορίου είναι επίσης μηδέν.

Τα αριθμητικά δεδομένα είναι εγγενώς ασταθή. Οποιαδήποτε μεταβλητή μπορεί να πάρει ένα σύνολο διαφορετικές αξίες. Για παράδειγμα, διαφορετικά αμοιβαία κεφάλαια έχουν διαφορετικά ποσοστά απόδοσης και ζημιών. Λόγω της μεταβλητότητας των αριθμητικών δεδομένων, είναι πολύ σημαντικό να μελετηθούν όχι μόνο εκτιμήσεις του μέσου όρου, οι οποίες έχουν αθροιστικό χαρακτήρα, αλλά και εκτιμήσεις της διακύμανσης, που χαρακτηρίζουν τη διασπορά των δεδομένων.

Η διακύμανση και η τυπική απόκλιση μας επιτρέπουν να εκτιμήσουμε την εξάπλωση των δεδομένων γύρω από τον μέσο όρο, με άλλα λόγια, να καθορίσουμε πόσα στοιχεία του δείγματος είναι λιγότερα από το μέσο όρο και πόσα είναι μεγαλύτερα. Η διασπορά έχει μερικές πολύτιμες μαθηματικές ιδιότητες. Ωστόσο, η τιμή του είναι το τετράγωνο μιας μονάδας μέτρησης - ένα τετραγωνικό ποσοστό, ένα τετραγωνικό δολάριο, μια τετραγωνική ίντσα κ.λπ. Επομένως, μια φυσική εκτίμηση της διακύμανσης είναι η τυπική απόκλιση, η οποία εκφράζεται στις συνήθεις μονάδες μέτρησης - ποσοστό εισοδήματος, δολάρια ή ίντσες.

Η τυπική απόκλιση σάς επιτρέπει να υπολογίσετε το μέγεθος της διακύμανσης των στοιχείων του δείγματος γύρω από τη μέση τιμή. Σχεδόν σε όλες τις περιπτώσεις, η πλειονότητα των παρατηρούμενων τιμών βρίσκεται εντός συν ή πλην μίας τυπικής απόκλισης από τη μέση τιμή. Επομένως, γνωρίζοντας τον αριθμητικό μέσο όρο των στοιχείων του δείγματος και την τυπική απόκλιση του δείγματος, είναι δυνατό να προσδιοριστεί το διάστημα στο οποίο ανήκει ο κύριος όγκος των δεδομένων.

Η τυπική απόκλιση των αποδόσεων σε 15 αμοιβαία κεφάλαια πολύ υψηλού κινδύνου είναι 6,6 (Εικόνα 9). Αυτό σημαίνει ότι η κερδοφορία του μεγαλύτερου μέρους των κεφαλαίων διαφέρει από τη μέση αξία κατά όχι περισσότερο από 6,6% (δηλαδή, κυμαίνεται στο εύρος από – Σ= 6,2 – 6,6 = –0,4 έως + Σ= 12,8). Μάλιστα, αυτό το διάστημα περιέχει μέση ετήσια απόδοση 53,3% (8 στα 15) πενταετίας.

Ρύζι. 9. Τυπική απόκλιση

Σημειώστε ότι κατά τη διαδικασία άθροισης των τετραγωνικών διαφορών, τα στοιχεία που είναι πιο μακριά από τη μέση κερδίζουν περισσότερο βάρος από τα στοιχεία που είναι πιο κοντά. Αυτή η ιδιότητα είναι ο κύριος λόγος για τον οποίο ο αριθμητικός μέσος όρος χρησιμοποιείται συχνότερα για την εκτίμηση του μέσου όρου μιας κατανομής.

Ο συντελεστής διακύμανσης

Σε αντίθεση με προηγούμενες εκτιμήσεις διασποράς, ο συντελεστής διακύμανσης είναι μια σχετική εκτίμηση. Μετριέται πάντα ως ποσοστό, όχι στις αρχικές μονάδες δεδομένων. Ο συντελεστής διακύμανσης, που συμβολίζεται με τα σύμβολα CV, μετρά τη διασπορά των δεδομένων γύρω από τη μέση τιμή. Ο συντελεστής διακύμανσης είναι ίσος με την τυπική απόκλιση διαιρούμενη με τον αριθμητικό μέσο όρο και πολλαπλασιαζόμενη επί 100%:

όπου μικρό- τυπική απόκλιση δείγματος, - μέσος όρος δείγματος.

Ο συντελεστής διακύμανσης σας επιτρέπει να συγκρίνετε δύο δείγματα, τα στοιχεία των οποίων εκφράζονται σε διαφορετικές μονάδες μέτρησης. Για παράδειγμα, ο διαχειριστής μιας υπηρεσίας παράδοσης αλληλογραφίας σκοπεύει να αναβαθμίσει τον στόλο των φορτηγών. Κατά τη φόρτωση συσκευασιών, υπάρχουν δύο τύποι περιορισμών που πρέπει να ληφθούν υπόψη: το βάρος (σε λίβρες) και ο όγκος (σε κυβικά πόδια) κάθε συσκευασίας. Ας υποθέσουμε ότι σε ένα δείγμα 200 σακουλών, το μέσο βάρος είναι 26,0 λίβρες, η τυπική απόκλιση του βάρους είναι 3,9 λίβρες, ο μέσος όγκος συσκευασίας είναι 8,8 κυβικά πόδια και η τυπική απόκλιση του όγκου είναι 2,2 κυβικά πόδια. Πώς να συγκρίνετε το spread του βάρους και του όγκου των πακέτων;

Δεδομένου ότι οι μονάδες μέτρησης για το βάρος και τον όγκο διαφέρουν μεταξύ τους, ο διαχειριστής πρέπει να συγκρίνει τη σχετική διασπορά αυτών των τιμών. Ο συντελεστής διακύμανσης βάρους είναι CV W = 3,9 / 26,0 * 100% = 15%, και ο συντελεστής διακύμανσης όγκου CV V = 2,2 / 8,8 * 100% = 25% . Έτσι, η σχετική διασπορά των όγκων πακέτων είναι πολύ μεγαλύτερη από τη σχετική διασπορά των βαρών τους.

Φόρμα διανομής

Η τρίτη σημαντική ιδιότητα του δείγματος είναι η μορφή της κατανομής του. Αυτή η κατανομή μπορεί να είναι συμμετρική ή ασύμμετρη. Για να περιγραφεί το σχήμα μιας κατανομής, είναι απαραίτητο να υπολογιστεί ο μέσος όρος και η διάμεσος. Εάν αυτά τα δύο μέτρα είναι τα ίδια, η μεταβλητή λέγεται ότι είναι συμμετρικά κατανεμημένη. Εάν η μέση τιμή μιας μεταβλητής είναι μεγαλύτερη από τη διάμεσο, η κατανομή της έχει θετική λοξότητα (Εικ. 10). Εάν η διάμεσος είναι μεγαλύτερη από τη μέση, η κατανομή της μεταβλητής είναι αρνητικά λοξή. Η θετική λοξότητα εμφανίζεται όταν ο μέσος όρος αυξάνεται σε ασυνήθιστα υψηλές τιμές. Η αρνητική λοξότητα εμφανίζεται όταν ο μέσος όρος μειώνεται σε ασυνήθιστα μικρές τιμές. Μια μεταβλητή κατανέμεται συμμετρικά εάν δεν λάβει ακραίες τιμές προς οποιαδήποτε κατεύθυνση, έτσι ώστε οι μεγάλες και οι μικρές τιμές της μεταβλητής να αλληλοεξουδετερώνονται.

Ρύζι. 10. Τρεις τύποι διανομών

Τα δεδομένα που απεικονίζονται στην κλίμακα Α έχουν αρνητική λοξότητα. Αυτό το σχήμα δείχνει μια μακριά ουρά και μια αριστερή λοξή που προκαλείται από ασυνήθιστα μικρές τιμές. Αυτές οι εξαιρετικά μικρές τιμές μετατοπίζουν τη μέση τιμή προς τα αριστερά και γίνεται μικρότερη από τη διάμεση τιμή. Τα δεδομένα που εμφανίζονται στην κλίμακα Β κατανέμονται συμμετρικά. Το αριστερό και το δεξί μισό της κατανομής είναι οι κατοπτρικές τους εικόνες. Οι μεγάλες και οι μικρές τιμές εξισορροπούν η μία την άλλη και ο μέσος όρος και ο διάμεσος είναι ίσοι. Τα δεδομένα που εμφανίζονται στην κλίμακα Β έχουν θετική λοξότητα. Αυτό το σχήμα δείχνει μια μακριά ουρά και μια λοξή προς τα δεξιά, που προκαλούνται από την παρουσία ασυνήθιστα υψηλών τιμών. Αυτές οι πολύ μεγάλες τιμές μετατοπίζουν τον μέσο όρο προς τα δεξιά και γίνεται μεγαλύτερος από τον διάμεσο.

Στο Excel, μπορείτε να λάβετε περιγραφικά στατιστικά στοιχεία χρησιμοποιώντας το πρόσθετο Πακέτο ανάλυσης. Περάστε από το μενού Δεδομένα → Ανάλυση δεδομένων, στο παράθυρο που ανοίγει, επιλέξτε τη γραμμή Περιγραφικά στατιστικάκαι κάντε κλικ Εντάξει. Στο παράθυρο Περιγραφικά στατιστικάφροντίστε να υποδείξετε διάστημα εισαγωγής(Εικ. 11). Εάν θέλετε να δείτε περιγραφικά στατιστικά στοιχεία στο ίδιο φύλλο με τα αρχικά δεδομένα, επιλέξτε το κουμπί επιλογής διάστημα εξόδουκαι καθορίστε το κελί στο οποίο θέλετε να τοποθετήσετε την επάνω αριστερή γωνία των εμφανιζόμενων στατιστικών (στο παράδειγμά μας, $C$1). Εάν θέλετε να εξάγετε δεδομένα σε ένα νέο φύλλο ή σε ένα νέο βιβλίο εργασίας, απλώς επιλέξτε το κατάλληλο κουμπί επιλογής. Επιλέξτε το πλαίσιο δίπλα Τελικά στατιστικά στοιχεία. Προαιρετικά, μπορείτε επίσης να επιλέξετε Επίπεδο δυσκολίας,κ-ο μικρότερο καικ-ο μεγαλύτερος.

Εάν είναι σε κατάθεση Δεδομέναστην περιοχή Ανάλυσηδεν βλέπετε το εικονίδιο Ανάλυση δεδομένων, πρέπει πρώτα να εγκαταστήσετε το πρόσθετο Πακέτο ανάλυσης(βλ., για παράδειγμα,).

Ρύζι. 11. Περιγραφικά στατιστικά στοιχεία των πενταετών μέσων ετήσιων αποδόσεων κεφαλαίων με πολύ υψηλά επίπεδα κινδύνου, που υπολογίζονται με τη χρήση του πρόσθετου Ανάλυση δεδομένωνΠρογράμματα Excel

Το Excel υπολογίζει έναν αριθμό στατιστικών που συζητήθηκαν παραπάνω: μέσος όρος, διάμεσος, τρόπος, τυπική απόκλιση, διακύμανση, εύρος ( διάστημα), ελάχιστο, μέγιστο και μέγεθος δείγματος ( έλεγχος). Επιπλέον, το Excel υπολογίζει ορισμένα νέα στατιστικά στοιχεία για εμάς: τυπικό σφάλμα, κύρτωση και λοξότητα. τυπικό σφάλμαισούται με την τυπική απόκλιση διαιρούμενη με την τετραγωνική ρίζα του μεγέθους του δείγματος. Ασυμμετρίαχαρακτηρίζει την απόκλιση από τη συμμετρία της κατανομής και είναι μια συνάρτηση που εξαρτάται από τον κύβο των διαφορών μεταξύ των στοιχείων του δείγματος και της μέσης τιμής. Η κούρτωση είναι ένα μέτρο της σχετικής συγκέντρωσης δεδομένων γύρω από τον μέσο όρο σε σχέση με τις ουρές της κατανομής και εξαρτάται από τις διαφορές μεταξύ του δείγματος και του μέσου όρου που αυξάνεται στην τέταρτη ισχύ.

Υπολογισμός περιγραφικών στατιστικών για το γενικό πληθυσμό

Ο μέσος όρος, η διασπορά και το σχήμα της κατανομής που συζητήθηκαν παραπάνω είναι χαρακτηριστικά που βασίζονται σε δείγμα. Ωστόσο, εάν το σύνολο δεδομένων περιέχει αριθμητικές μετρήσεις ολόκληρου του πληθυσμού, τότε οι παράμετροί του μπορούν να υπολογιστούν. Αυτές οι παράμετροι περιλαμβάνουν τον μέσο όρο, τη διακύμανση και την τυπική απόκλιση του πληθυσμού.

Αναμενόμενη αξίαισούται με το άθροισμα όλων των τιμών του γενικού πληθυσμού διαιρεμένο με τον όγκο του γενικού πληθυσμού:

όπου µ - αναμενόμενη αξία, ΧΕγώ- Εγώ-η μεταβλητή παρατήρηση Χ, Ν- τον όγκο του γενικού πληθυσμού. Στο Excel, για τον υπολογισμό της μαθηματικής προσδοκίας, χρησιμοποιείται η ίδια συνάρτηση με τον αριθμητικό μέσο όρο: =AVERAGE().

Διακύμανση πληθυσμούίσο με το άθροισμα των τετραγωνικών διαφορών μεταξύ των στοιχείων του γενικού πληθυσμού και του ματ. προσδοκίες διαιρεμένες με το μέγεθος του πληθυσμού:

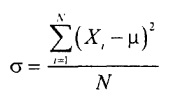
όπου σ2είναι η διακύμανση του γενικού πληθυσμού. Το Excel πριν από την έκδοση 2007 χρησιμοποιεί τη συνάρτηση =VAR() για να υπολογίσει τη διακύμανση του πληθυσμού, ξεκινώντας από την έκδοση 2010 =VAR.G().

τυπική απόκλιση πληθυσμούισούται με την τετραγωνική ρίζα της διακύμανσης του πληθυσμού:

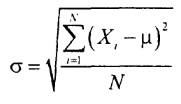
Το Excel πριν από την έκδοση 2007 χρησιμοποιεί το =STDEV() για τον υπολογισμό της τυπικής απόκλισης του πληθυσμού, ξεκινώντας με την έκδοση 2010 =STDEV.Y(). Σημειώστε ότι οι τύποι για τη διακύμανση πληθυσμού και την τυπική απόκλιση είναι διαφορετικοί από τους τύπους για τη διακύμανση του δείγματος και την τυπική απόκλιση. Κατά τον υπολογισμό των στατιστικών δειγμάτων S2και μικρόο παρονομαστής του κλάσματος είναι n - 1, και κατά τον υπολογισμό των παραμέτρων σ2και σ - τον όγκο του γενικού πληθυσμού Ν.

εμπειρικός κανόνας

Στις περισσότερες περιπτώσεις, ένα μεγάλο ποσοστό παρατηρήσεων συγκεντρώνεται γύρω από τη διάμεσο, σχηματίζοντας ένα σύμπλεγμα. Σε σύνολα δεδομένων με θετική λοξότητα, αυτό το σύμπλεγμα βρίσκεται στα αριστερά (δηλαδή, κάτω) της μαθηματικής προσδοκίας και σε σύνολα με αρνητική λοξότητα, αυτό το σύμπλεγμα βρίσκεται στα δεξιά (δηλαδή, πάνω) της μαθηματικής προσδοκίας. Τα συμμετρικά δεδομένα έχουν τον ίδιο μέσο όρο και διάμεσο, και οι παρατηρήσεις συγκεντρώνονται γύρω από το μέσο όρο, σχηματίζοντας μια κατανομή σε σχήμα καμπάνας. Εάν η κατανομή δεν έχει έντονη λοξότητα και τα δεδομένα συγκεντρώνονται γύρω από ένα συγκεκριμένο κέντρο βάρους, μπορεί να χρησιμοποιηθεί ένας εμπειρικός κανόνας για την εκτίμηση της μεταβλητότητας, ο οποίος λέει: εάν τα δεδομένα έχουν κατανομή σε σχήμα καμπάνας, τότε περίπου το 68% από τις παρατηρήσεις είναι μικρότερη από μία τυπική απόκλιση από τη μαθηματική προσδοκία, Περίπου το 95% των παρατηρήσεων είναι εντός δύο τυπικών αποκλίσεων από την αναμενόμενη τιμή και το 99,7% των παρατηρήσεων είναι εντός τριών τυπικών αποκλίσεων από την αναμενόμενη τιμή.

Έτσι, η τυπική απόκλιση, η οποία είναι μια εκτίμηση της μέσης διακύμανσης γύρω από τη μαθηματική προσδοκία, βοηθά στην κατανόηση του τρόπου κατανομής των παρατηρήσεων και στον προσδιορισμό των ακραίων τιμών. Από τον εμπειρικό κανόνα προκύπτει ότι για κατανομές σε σχήμα καμπάνας, μόνο μία τιμή στις είκοσι διαφέρει από τη μαθηματική προσδοκία κατά περισσότερες από δύο τυπικές αποκλίσεις. Επομένως, τιμές εκτός του διαστήματος μ ± 2σ, μπορούν να θεωρηθούν ακραίες τιμές. Επιπλέον, μόνο τρεις στις 1000 παρατηρήσεις διαφέρουν από τις μαθηματικές προσδοκίες κατά περισσότερες από τρεις τυπικές αποκλίσεις. Έτσι, τιμές εκτός του διαστήματος μ ± 3σείναι σχεδόν πάντα ακραίες. Για διανομές που είναι πολύ λοξές ή δεν έχουν σχήμα καμπάνας, μπορεί να εφαρμοστεί ο εμπειρικός κανόνας Biename-Chebyshev.

Πριν από περισσότερα από εκατό χρόνια, οι μαθηματικοί Bienamay και Chebyshev ανακάλυψαν ανεξάρτητα μια χρήσιμη ιδιότητα της τυπικής απόκλισης. Βρήκαν ότι για οποιοδήποτε σύνολο δεδομένων, ανεξάρτητα από το σχήμα της κατανομής, το ποσοστό των παρατηρήσεων που βρίσκονται σε απόσταση που δεν υπερβαίνει κτυπικές αποκλίσεις από τις μαθηματικές προσδοκίες, όχι λιγότερες (1 – 1/ 2)*100%.

Για παράδειγμα, εάν κ= 2, ο κανόνας Biename-Chebyshev δηλώνει ότι τουλάχιστον (1 - (1/2) 2) x 100% = 75% των παρατηρήσεων πρέπει να βρίσκονται στο διάστημα μ ± 2σ. Αυτός ο κανόνας ισχύει για οποιονδήποτε κυπερβαίνει το ένα. Ο κανόνας Biename-Chebyshev είναι πολύ γενικής φύσης και ισχύει για διανομές κάθε είδους. Υποδεικνύει τον ελάχιστο αριθμό παρατηρήσεων, η απόσταση από την οποία μέχρι τη μαθηματική προσδοκία δεν υπερβαίνει μια δεδομένη τιμή. Ωστόσο, εάν η κατανομή είναι σε σχήμα καμπάνας, ο εμπειρικός κανόνας εκτιμά με μεγαλύτερη ακρίβεια τη συγκέντρωση των δεδομένων γύρω από τη μέση τιμή.

Υπολογισμός περιγραφικών στατιστικών για μια κατανομή με βάση τη συχνότητα

Εάν τα αρχικά δεδομένα δεν είναι διαθέσιμα, η κατανομή συχνότητας γίνεται η μόνη πηγή πληροφοριών. Σε τέτοιες περιπτώσεις, μπορείτε να υπολογίσετε τις κατά προσέγγιση τιμές των ποσοτικών δεικτών της κατανομής, όπως ο αριθμητικός μέσος όρος, η τυπική απόκλιση, τα τεταρτημόρια.

Εάν τα δεδομένα του δείγματος παρουσιάζονται ως κατανομή συχνότητας, μπορεί να υπολογιστεί μια κατά προσέγγιση τιμή του αριθμητικού μέσου όρου, υποθέτοντας ότι όλες οι τιμές σε κάθε κατηγορία συγκεντρώνονται στο μέσο της κατηγορίας:

όπου - μέσος όρος δείγματος, n- αριθμός παρατηρήσεων ή μέγεθος δείγματος, Με- τον αριθμό των κλάσεων στην κατανομή συχνότητας, mj- μεσαίο σημείο ι-η τάξη, φάι- συχνότητα που αντιστοιχεί σε ι-η τάξη.

Για τον υπολογισμό της τυπικής απόκλισης από την κατανομή συχνότητας, θεωρείται επίσης ότι όλες οι τιμές σε κάθε κατηγορία συγκεντρώνονται στο μέσο της κατηγορίας.

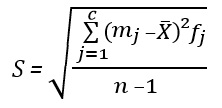
Για να κατανοήσουμε πώς καθορίζονται τα τεταρτημόρια της σειράς με βάση τις συχνότητες, ας εξετάσουμε τον υπολογισμό του κατώτερου τεταρτημορίου με βάση τα δεδομένα για το 2013 σχετικά με την κατανομή του ρωσικού πληθυσμού κατά μέσο κατά κεφαλήν εισόδημα σε μετρητά (Εικ. 12).

Ρύζι. 12. Το μερίδιο του πληθυσμού της Ρωσίας με κατά κεφαλήν νομισματικό εισόδημα κατά μέσο όρο ανά μήνα, ρούβλια

Για να υπολογίσετε το πρώτο τεταρτημόριο της σειράς παραλλαγής διαστήματος, μπορείτε να χρησιμοποιήσετε τον τύπο:

όπου Q1 είναι η τιμή του πρώτου τεταρτημορίου, xQ1 είναι το κατώτερο όριο του διαστήματος που περιέχει το πρώτο τεταρτημόριο (το διάστημα καθορίζεται από τη συσσωρευμένη συχνότητα, η πρώτη υπερβαίνει το 25%). i είναι η τιμή του διαστήματος. Σf είναι το άθροισμα των συχνοτήτων ολόκληρου του δείγματος. πιθανώς πάντα ίσο με 100%? SQ1–1 είναι η αθροιστική συχνότητα του διαστήματος που προηγείται του διαστήματος που περιέχει το κατώτερο τεταρτημόριο. fQ1 είναι η συχνότητα του διαστήματος που περιέχει το κατώτερο τεταρτημόριο. Ο τύπος για το τρίτο τεταρτημόριο διαφέρει στο ότι σε όλα τα μέρη, αντί για Q1, πρέπει να χρησιμοποιήσετε το Q3 και να αντικαταστήσετε το ¾ αντί για το ¼.

Στο παράδειγμά μας (Εικ. 12), το κατώτερο τεταρτημόριο είναι στην περιοχή 7000,1 - 10,000, η ​​αθροιστική συχνότητα του οποίου είναι 26,4%. Το κατώτερο όριο αυτού του διαστήματος είναι 7000 ρούβλια, η τιμή του διαστήματος είναι 3000 ρούβλια, η συσσωρευμένη συχνότητα του διαστήματος που προηγείται του διαστήματος που περιέχει το κάτω τεταρτημόριο είναι 13,4%, η συχνότητα του διαστήματος που περιέχει το κάτω τεταρτημόριο είναι 13,0%. Έτσι: Q1 \u003d 7000 + 3000 * (¼ * 100 - 13,4) / 13 \u003d 9677 ρούβλια.

Παγίδες που σχετίζονται με περιγραφικές στατιστικές

Σε αυτό το σημείωμα, εξετάσαμε πώς να περιγράψουμε ένα σύνολο δεδομένων χρησιμοποιώντας διάφορα στατιστικά στοιχεία που εκτιμούν τον μέσο όρο, τη διασπορά και την κατανομή του. Το επόμενο βήμα είναι η ανάλυση και η ερμηνεία των δεδομένων. Μέχρι στιγμής, μελετήσαμε τις αντικειμενικές ιδιότητες των δεδομένων και τώρα στραφούμε στην υποκειμενική ερμηνεία τους. Δύο λάθη περιμένουν τον ερευνητή: ένα εσφαλμένα επιλεγμένο θέμα ανάλυσης και μια εσφαλμένη ερμηνεία των αποτελεσμάτων.

Η ανάλυση της απόδοσης 15 αμοιβαίων κεφαλαίων πολύ υψηλού κινδύνου είναι αρκετά αμερόληπτη. Οδήγησε σε εντελώς αντικειμενικά συμπεράσματα: όλα τα αμοιβαία κεφάλαια έχουν διαφορετικές αποδόσεις, το spread των αποδόσεων των αμοιβαίων κεφαλαίων κυμαίνεται από -6,1 έως 18,5 και η μέση απόδοση είναι 6,08. Η αντικειμενικότητα της ανάλυσης δεδομένων διασφαλίζεται από τη σωστή επιλογή των συνολικών ποσοτικών δεικτών της κατανομής. Εξετάστηκαν διάφορες μέθοδοι για την εκτίμηση του μέσου όρου και της διασποράς των δεδομένων και αναφέρθηκαν τα πλεονεκτήματα και τα μειονεκτήματά τους. Πώς να επιλέξετε τα σωστά στατιστικά στοιχεία που παρέχουν μια αντικειμενική και αμερόληπτη ανάλυση; Εάν η κατανομή των δεδομένων είναι ελαφρώς λοξή, πρέπει να επιλεγεί η διάμεσος έναντι του αριθμητικού μέσου όρου; Ποιος δείκτης χαρακτηρίζει με μεγαλύτερη ακρίβεια την εξάπλωση των δεδομένων: τυπική απόκλιση ή εύρος; Πρέπει να αναφέρεται η θετική λοξότητα της κατανομής;

Από την άλλη πλευρά, η ερμηνεία δεδομένων είναι μια υποκειμενική διαδικασία. Διαφορετικοί άνθρωποι καταλήγουν σε διαφορετικά συμπεράσματα, ερμηνεύοντας τα ίδια αποτελέσματα. Ο καθένας έχει τη δική του άποψη. Κάποιος θεωρεί ότι οι συνολικές μέσες ετήσιες αποδόσεις 15 αμοιβαίων κεφαλαίων με πολύ υψηλό επίπεδο κινδύνου είναι καλές και είναι αρκετά ικανοποιημένος με το εισόδημα που εισπράττει. Άλλοι μπορεί να πιστεύουν ότι αυτά τα κεφάλαια έχουν πολύ χαμηλές αποδόσεις. Έτσι, η υποκειμενικότητα θα πρέπει να αντισταθμίζεται από την ειλικρίνεια, την ουδετερότητα και τη σαφήνεια των συμπερασμάτων.

Ηθικά ζητήματα

Η ανάλυση δεδομένων είναι άρρηκτα συνδεδεμένη με ηθικά ζητήματα. Κάποιος πρέπει να είναι επικριτικός απέναντι στις πληροφορίες που διαδίδονται από τις εφημερίδες, το ραδιόφωνο, την τηλεόραση και το Διαδίκτυο. Με τον καιρό, θα μάθετε να είστε δύσπιστοι όχι μόνο για τα αποτελέσματα, αλλά και για τους στόχους, το αντικείμενο και την αντικειμενικότητα της έρευνας. Ο διάσημος Βρετανός πολιτικός Benjamin Disraeli το είπε καλύτερα: «Υπάρχουν τρία είδη ψεμάτων: ψέματα, καταραμένα ψέματα και στατιστικές».

Όπως σημειώνεται στη σημείωση, προκύπτουν ηθικά ζητήματα κατά την επιλογή των αποτελεσμάτων που πρέπει να παρουσιάζονται στην έκθεση. Θα πρέπει να δημοσιεύονται τόσο τα θετικά όσο και τα αρνητικά αποτελέσματα. Επιπλέον, όταν κάνετε μια αναφορά ή γραπτή αναφορά, τα αποτελέσματα πρέπει να παρουσιάζονται ειλικρινά, ουδέτερα και αντικειμενικά. Διακρίνετε τις κακές και τις ανέντιμες παρουσιάσεις. Για να γίνει αυτό, είναι απαραίτητο να προσδιοριστούν ποιες ήταν οι προθέσεις του ομιλητή. Μερικές φορές ο ομιλητής παραλείπει σημαντικές πληροφορίες από άγνοια, και μερικές φορές εσκεμμένα (για παράδειγμα, εάν χρησιμοποιεί τον αριθμητικό μέσο όρο για να εκτιμήσει τον μέσο όρο των σαφώς λοξών δεδομένων για να πάρει το επιθυμητό αποτέλεσμα). Είναι επίσης ανέντιμο να καταστείλουμε αποτελέσματα που δεν ανταποκρίνονται στην άποψη του ερευνητή.

Χρησιμοποιούνται υλικά από το βιβλίο Levin et al Στατιστικά για μάνατζερ. - Μ.: Williams, 2004. - Σελ. 178–209

Η συνάρτηση QUARTILE διατηρήθηκε για ευθυγράμμιση με προηγούμενες εκδόσεις του Excel